adc reference voltage is less than what i want to measure
Using a 12-chip-resolution analog-to-digital converter (ADC) does not necessarily hateful your system volition have 12-bit accurateness. Sometimes, much to the surprise and consternation of engineers, a information-conquering system volition exhibit much lower performance than expected. When this is discovered afterward the initial epitome run, a mad scramble for a higher-performance ADC ensues, and many hours are spent reworking the design as the deadline for preproduction builds fast approaches. What happened? What changed from the initial assay? A thorough agreement of ADC specifications will reveal subtleties that often lead to less-than-desired performance. Agreement ADC specifications volition besides help yous in selecting the correct ADC for your application.
We start past establishing our overall system-performance requirements. Each component in the arrangement will accept an associated mistake; the goal is to go along the total error beneath a certain limit. Often the ADC is the key component in the betoken path, so we must be careful to select a suitable device. For the ADC, permit'south assume that the conversion-rate, interface, power-supply, power-dissipation, input-range, and channel-count requirements are adequate earlier we begin our evaluation of the overall system performance. Accuracy of the ADC is dependent on several key specs, which include integral nonlinearity error (INL), offset and gain errors, and the accurateness of the voltage reference, temperature effects, and AC operation. It is usually wise to brainstorm the ADC assay by reviewing the DC operation, because ADCs use a plethora of nonstandardized test weather for the Air conditioning operation, making information technology easier to compare two ICs based on DC specifications. The DC performance will in general be ameliorate than the AC functioning.
Organization Requirements
Two popular methods for determining the overall organization error are the root-sum-square (RSS) method and the worst-instance method. When using the RSS method, the error terms are individually squared, so added, and then the foursquare root is taken. The RSS mistake budget is given by:
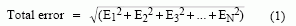
where ENorth represents the term for a particular circuit component or parameter. This method is most accurate when the all error terms are uncorrelated (which may or may not be the example). With worst-case error analysis, all error terms add. This method guarantees the error volition never exceed a specified limit. Sinceit sets the limit of how bad the error tin exist, the actual error is always less than this value (often-times MUCH less).
The measured error is usually somewhere betwixt the values given by the 2 methods, simply is often closer to the RSS value. Notation that depending on one's error budget, typical or worst-case values for the mistake terms can be used. The decision is based on many factors, including the standard deviation of the measurement value, the importance of that particular parameter, the size of the mistake in relation to other errors, etc. So there really aren't difficult and fast rules that must be obeyed. For our analysis, we will use the worst-case method.
In this example, let'due south presume we need 0.1% or 10 bits of accurateness (one/210), so it makes sense to choose a converter with greater resolution than this. If nosotros select a 12-scrap converter, we can assume it will be adequate; but without reviewing the specifications, in that location is no guarantee of 12-bit performance (it may be ameliorate or worse). For example, a 12-bit ADC with 4LSBs of integral nonlinearity error tin requite only 10 bits of accuracy at best (bold the offset and gain errors have been calibrated). A device with 0.5LSBs of INL can requite 0.0122% error or thirteen bits of accuracy (with gain and offset errors removed). To calculate best-case accuracy, split the maximum INL error by iiN, where N is the number of bits. In our example, allowing 0.075% fault (or 11 bits) for the ADC leaves 0.025% fault for the remainder of the circuitry, which will include errors from the sensor, the associated front-end signal conditioning circuitry (op amps, multiplexers, etc.), and perhaps digital-to-analog converters (DACs), PWM signals, or other analog-output signals in the indicate path.
We assume that the overall system will have a total-fault budget based on the summation of error terms for each excursion component in the signal path. Other assumptions we volition brand are that we are measuring a deadening-irresolute, DC-blazon, bipolar input bespeak with a 1kHz bandwidth and that our operating temperature range is 0°C to 70°C with functioning guaranteed from 0°C to 50°C.
DC Performance
Differential nonlinearity
Though non mentioned equally a cardinal parameter for an ADC, the differential nonlinearity (DNL) error is the first specification to detect. DNL reveals how far a lawmaking is from a neighboring code. The distance is measured as a change in input-voltage magnitude and and then converted to LSBs (Figure 1). Note that INL is the integral of the DNL errors, which is why DNL is non included in our list of key parameters. The key for good performance for an ADC is the merits "no missing codes." This means that, as the input voltage is swept over its range, all output lawmaking combinations will appear at the converter output. A DNL error of <±1LSB guarantees no missing codes (Figure 1a). In Figures 1b, 1c, and 1d, three DNL mistake values are shown. With a DNL error of -0.5LSB (Figure 1b), the device is guaranteed to have no missing codes. With a value equal to -1LSB (Figure 1c), the device is non necessarily guaranteed to take no missing codes. Note that lawmaking 10 is missing. Yet, most ADCs that specify a maximum DNL error of +/-1 volition specifically land whether the device has missing codes or not. Because the production-examination limits are actually tighter than the information-sheet limits, no missing codes is ordinarily guaranteed. With a DNL value greater than -1 (-1.5LSB in Figure 1d), the device has missing codes.

Figure 1b. DNL error: no missing codes.
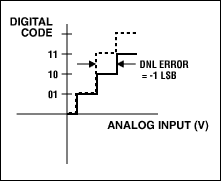
Figure 1c. DNL fault: Code 10 is missing.

Effigy 1d. DNL error: At AIN* the digital lawmaking tin can be 1 of three possible values. When the input voltage is swept, Code 10 will be missing.
When DNL-fault values are showtime (that is, -1LSB, +2LSB), the ADC transfer function is altered. Showtime DNL values can still in theory have no missing codes. The key is having -1LSB as the low limit. Annotation that DNL is measured in one management, usually going up the transfer function. The input-voltage level required to create the transition at lawmaking [N] is compared to that at lawmaking [Northward+1]. If the difference is 1LSB autonomously, the DNL fault is zero. If it is greater than 1LSB, the DNL error is positive; if it is less than 1LSB, the DNL mistake is negative.
Having missing codes is not necessarily bad. If you demand but thirteen bits of resolution and you have a choice between a 16-bit ADC with a DNL specification < = +/-4LSB DNL (which is effectively 14 bits, no missing codes) that costs $5 and a 16-bit ADC with a DNL of < = +/-1LSB that costs $15, then buying the lower-class version of the ADC will allow you to greatly reduce component cost and still meet your system requirements.
INL
INL is divers as the integral of the DNL errors, so good INL guarantees adept DNL. The INL error tells how far away from the ideal transfer-office value the measured converter result is. Continuing with our example, an INL error of +/-2LSB in a 12-bit organisation ways the maximum nonlinearity error may exist off by two/4096 or 0.05% (which is already almost two-thirds of the allotted ADC error budget). Thus, a 1LSB (or better) part is required. With a +/-1LSB INL error, the accuracy is 0.0244%, which accounts for 32.five% of the allotted ADC fault budget. With a specification of 0.5LSB, the accurateness is 0.012%, and this accounts for but most sixteen% (0.012%/0.075%) of our ADC mistake budget limit. Note that neither INL nor DNL errors tin be calibrated or corrected easily.
Offset and Gain Errors
Offset and proceeds errors tin can easily be calibrated out using a microcontroller (µC) or a digital signal processor (DSP). With outset fault, the measurement is unproblematic when the converter allows bipolar input signals. In bipolar systems, outset error shifts the transfer function but does not reduce the number of available codes (Figure 2). At that place are two methodologies to zero out bipolar errors. In 1, you shift the ten and y axes of the transfer part and then that the negative total-scale point aligns with the zero point of a unipolar system (Figure 3a). With this technique, you but remove the commencement fault and and then adjust for gain error by rotating the transfer part near the "new" zero point. The second technique entails using an iterative arroyo. Kickoff utilise zero volts to the ADC input and perform a conversion; the conversion result represents the bipolar nada offset error. Then perform a gain adjustment by rotating the curve about the negative full-calibration betoken (Effigy 3b). Note that the transfer function has pivoted around point A, which moves the zippo point away from the desired transfer part. Thus, a subsequent offset-error calibration may be required.
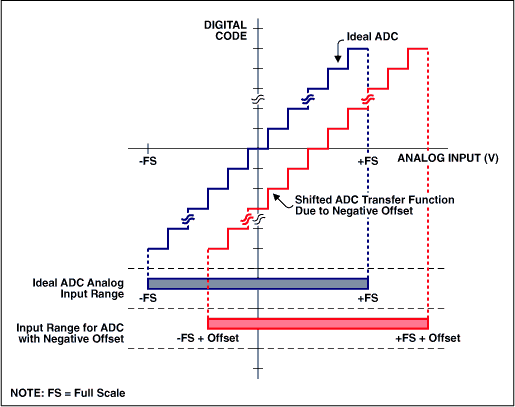
Figure 2. Bipolar get-go error.
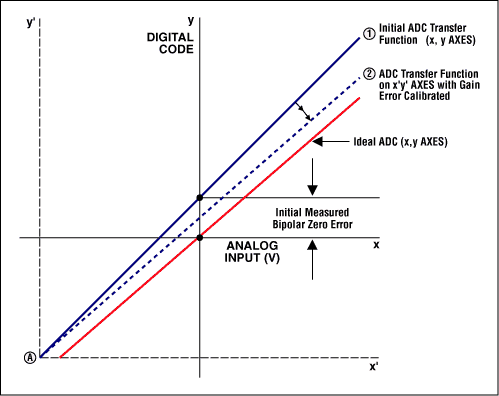
Figure 3a.
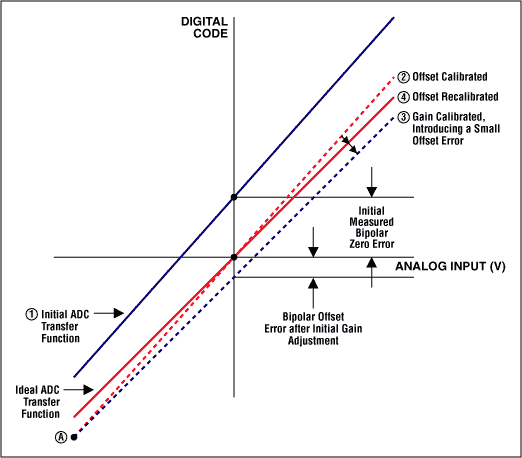
Figure 3b.
Figures 3a and 3b. Calibrating bipolar get-go error. (Note: The stair-footstep transfer function has been replaced past a straight line, because this graph shows all codes and the step size is so small that the line appears to exist linear.)
Unipolar systems are a little trickier. If the get-go is positive, utilize the same methodology as that for bipolar supplies. The departure hither is that you lose part of the ADC's range (run across Figure four). If the offset is negative, you cannot simply do a conversion and expect the issue to represent the offset mistake. Below goose egg, the converter will just brandish zeros. Thus, with a negative offset error, you must increase the input voltage slowly to determine where the beginning ADC transition occurs. Hither over again yous lose office of the ADC range.

Effigy 4. Unipolar get-go error.
Returning to our case, 2 scenarios for outset error are given below:
- If the offset error is +8mV, with a 2.5V reference this corresponds to 13LSBs of error for a 12-flake ADC (8mV/[2.5V/4096)]. Though the resolution is however 12 bits, you must subtract thirteen codes from each conversion result to recoup for the offset error. Note that the actual, measurable, total-scale value in this scenario is at present 2.5V (4083/4096) = 2.492V. Whatever value above this volition over-range the ADC. So, the dynamic range, or range of input values, for the ADC has been reduced. This is even more important for higher-resolution ADCs; 8mV represents 210LSBs at the 16-bit level (VREF = 2.5V).
- If the offset is -8mV (assuming a unipolar input), and so minor analog-input values virtually zippo volition non register when a conversion is performed until the analog input exceeds +8mV. This besides reduces the dynamic range of the ADC.
Gain error is divers as the full-scale error minus the offset error (Figure v). Full-scale error is measured at the concluding ADC transition on the transfer-function curve and compared against the ideal ADC transfer function. Gain error is easily corrected in software with a linear function y = (m1/m2)(10), where m1 is the gradient of the platonic transfer function and m2 is the slope of the measured transfer function (Figure five).

Figure 5. Offset, gain, and total-calibration errors.
The proceeds-error specification may or may not include errors contributed by the ADC's voltage reference. In the electrical specifications, information technology is important to check the weather condition to encounter how gain mistake is tested and to decide whether information technology is performed with an internal or external reference. Typically, the gain fault is much worse when an on-flake reference is used. If the gain error were zero, when a conversion is performed the conversion issue would begin to yield all ones (3FFh in our 12-flake example) when the full-scale analog input is practical (see Effigy half-dozen). As our converter is not ideal, you can initially end up with all ones in the conversion outcome when a voltage greater than full-calibration is practical (negative gain mistake) or when a voltage less than full-scale is applied (positive proceeds error). Two ways to arrange for gain mistake are to either tweak the reference voltage such that at a specific reference-voltage value the output gives full-calibration or utilize a linear correction curve in software to alter the slope of the ADC transfer-function curve (a get-go-society linear equation or a lookup tabular array tin can be used).
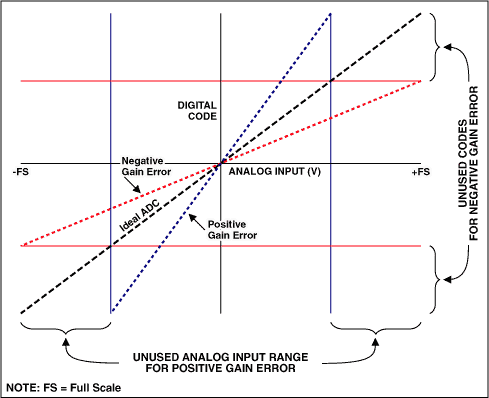
Figure six. Gain error reduces dynamic range.
As with get-go error, you lot lose dynamic range with gain error. For example, if a full-calibration input voltage is practical and the lawmaking obtained is 4050 instead of the ideal 4096 (for a 12-scrap converter), this is defined as negative gain mistake, and in this case the upper 46 codes will non be used. Similarly, if the full-scale code of 4096 appears with an input voltage less than full-scale, the ADC's dynamic range is again reduced (meet Figure 6). Note that, with positive full-scale errors, you cannot calibrate beyond the point where the converter gives all ones in the conversion result.
The easiest manner to handle offset and gain errors is to find an ADC with values low enough and then that you lot don't have to calibrate. Information technology'southward fairly easy to notice 12-fleck ADCs with offset and gain errors less than 4LSB.
Other Subtle Error Sources
Lawmaking-Edge Noise
Code-edge noise is the amount of noise that appears right at a lawmaking transition on the transfer function. It is oft non specified in the data sheet. Fifty-fifty higher-resolution converters (sixteen+ bits), where code-edge racket is much more prevalent due to the smaller LSB size, will often not specify lawmaking-edge noise. Sometimes, code-edge racket can be several LSBs. Conversions performed with the analog input right at the code edge can result in code flicker in the LSBs. Meaning lawmaking-edge racket means that an average of samples must be taken to finer remove this noise from the converter results. How many samples are needed? If the code-edge noise is two/3LSB RMS, this equates to approximately 4LSB p-p. 16 samples volition accept to exist taken to reduce the noise to 1LSB (the square root of the number of samples determines the comeback in operation).
The Reference
One of the biggest potential sources of errors in an ADC with an internal or external reference is the reference voltage. Often, if the reference is included on-chip, information technology is not specified adequately. To empathize the source of the reference errors, it is important to look at three specs in particular: temperature drift, voltage noise, and load regulation.
Temperature Migrate
Temperature drift is the most overlooked specification in the information sheet. As an instance, note how temperature drift affects the performance of an ADC converter based on resolution (Figure 7). For a 12-bit converter to maintain accuracy over the extended temperature range (-40°C to +85°C), the drift must be a maximum of 4ppm/°C. Unfortunately, no ADC converter is bachelor with this kind of on-chip-reference functioning. If nosotros relax the requirements, a 10-degree temperature excursion means the 12-scrap ADC reference tin can drift no more 25ppm/°C, which once again is a fairly tight requirement for on-chip references. Prototyping frequently does not reveal the significance of this error, considering parts are oft from a similar lot and thus the test results do not take into account the extremes that occur in specs due to manufacturing-process variations.

Effigy 7. Voltage-reference-migrate requirements chronicle to ADC resolution.
For some systems, the reference accurateness is non a big issue, as the temperature is held constant, eliminating the drift problem. Some systems use a ratiometric measurement, where the reference errors are removed because the aforementioned signal that excites the sensor is used as the reference voltage (Figure eight). Because the excitation source and reference move as 1, drift errors are eliminated.

Figure eight. Ratiometric ADC conversion.
In other systems, scale is performed often enough so that reference drift is finer removed. In still other systems, accented accurateness is not disquisitional, merely relative accuracy is. Therefore, the reference can migrate slowly with time and the system will provide the desired accuracy.
Voltage Racket
Another important spec is voltage noise. It is often specified as either an RMS value or a peak-to-superlative value. Convert the RMS value to a peak-to-meridian value to evaluate its effect on functioning. If a 2.5V reference has 500µV of peak-to-peak voltage noise at the output (or 83µV RMS), this noise represents 0.02% error or barely 12-bit operation, and this is before any of the converter errors are considered. Ideally, our reference-racket operation should exist a small fraction of an LSB so as non to limit the ADC's performance. ADCs with on-chip references ordinarily don't specify voltage noise, then the error is up to the user to decide. If you are not getting the performance yous desire and are using an internal reference, attempt using a very good external reference to determine if the on-chip reference is in fact the culprit.
Load Regulation
The final spec is reference load regulation. Oft the voltage reference used for an ADC has aplenty current to drive other devices, so it is used past other ICs. The current drawn past those other components volition affect the voltage reference, which means that every bit more than current is drawn the reference voltage will droop. If the devices using the reference are turning on and off intermittently, the effect will exist a reference voltage that moves up and down. A 0.55µV/µA reference-load-regulation specification for a 2.5V reference means that, if other devices draw 800µA, the reference voltage volition change up to 440µV, which is .0176% (440µV/2.5V) or almost 20% of the available error margin.
Other Temperature Effects
Continuing with the topic of temperature, two specifications that are often given picayune attention are offset drift and gain migrate. These specs are usually given as typical numbers only, leaving information technology up to the users to determine if the specification is good plenty for their organization requirements. Offset- and proceeds-drift values tin can be compensated in a couple of different ways. One way is to fully characterize the offset and gain migrate, and provide a lookup table in memory to suit the values as temperature changes. This, however, is a cumbersome process, as each ADC must be compensated individually and the compensation procedure is a time-consuming effort. The second method is to perform calibrations when a significant temperature change has occurred.
With systems that practise a i-time temperature calibration, it's important to pay heed to the drift specs. If the initial offset is calibrated and the temperature moves, at that place will exist an error introduced due to the drift term that can negate the furnishings of the scale. For example, assume a reading is done at temperature 10. Some time later, the temperature has changed 10°C and the exact same measurement is taken. These two readings can give different results, calling into question the repeatability and thus the reliability of the arrangement.
There is a practiced reason why manufacturers exercise not requite maximum limits: This increases the toll. Drift testing requires special boards, and an extra footstep must be added to the test flow (which equates to an boosted manufacturing cost) to brand sure the parts do not exceed the maximum-drift limit.
Gain drift is more of an issue, particularly for devices tested with an internal reference. In this case, the reference drift can be included in the gain-drift parameter. For an external reference, the IC's gain drift is typically adequately small-scale, like 0.8ppm/°C. Thus, a +/-10 degree temperature change results in a +/-8ppm change. Notation that 12-flake performance equates to 244ppm (i/4096 = 0.0244% = 244ppm). So, we come across an error that represents only a fraction of an LSB at the 12-bit level.
AC Functioning
Some ADCs perform well only with input signals at or virtually DC. Others perform well with input signals from DC upwards to Nyquist. Simply because DNL and INL meet the system requirements does not mean the converter volition give that same operation when Air-conditioning signals are considered. DNL and INL are DC tests. Nosotros must look to the Air conditioning specs to become a good feeling for Ac operation. The Electrical Characteristics table and the Typical Operating Characteristics found in the information sheet offering clues to the AC performance. The key specs to review are betoken-to-noise ratio (SNR), signal-to-noise and distortion ratio (SINAD), total harmonic distortion (THD), and spurious-free dynamic range (SFDR). The first specification to review is SINAD or SNR. SINAD is defined as the RMS value of an input sine moving ridge to the RMS value of the racket of the converter (from DC to the Nyquist frequency, including harmonic [total harmonic baloney] content). Harmonics occur at multiples of the input frequency (run into Effigy 9). SNR is similar to SINAD, except that information technology does non include the harmonic content. Thus, the SNR should always be ameliorate than the SINAD. Both SINAD and SNR are typically expressed in dB.

where Northward is the number of bits. For an platonic 12-bit converter, the SINAD is 74dB. Should this equation be rewritten in terms of N, it would reveal how many bits of information are obtained as a function of the RMS dissonance:
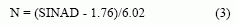
This equation is the definition for constructive number of bits, or ENOB.
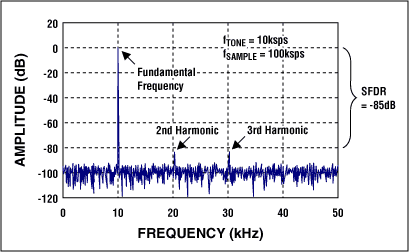
Figure 9. FFT plot reveals Air conditioning operation of an ADC.
Note that SINAD is a function of the input frequency. As frequency increases toward the Nyquist limit, SINAD decreases. If the specification in the data sheet is tested at low frequencies compared to the Nyquist frequency, you can bet the performance will exist much worse almost Nyquist. Wait for an ENOB graph in the Typical Operating Characteristics of the data sheet. ENOB degrades with frequency primarily because THD gets increasingly worse as the input frequency increases. For example, with a SINAD minimum value of 68dB at the frequency of interest, y'all obtain an ENOB value of 11. Therefore, you accept lost one flake of information due to the converter's racket and baloney performance. This means that your 12-bit converter tin can provide only 0.05% accurateness at best. Call back that INL is a DC spec; ENOB is the specification that tells about nonlinearities for Ac signals.
SNR is the signal-to-noise ratio with the distortion components removed. SNR reveals where the noise floor of the converter is. In that location can exist a steep decrease in SNR as a part of input frequency, which ways the converter was not designed for frequencies well-nigh this signal. One way to improve SNR is to oversample, which provides a processing proceeds. Oversampling is a method of lowering the noise floor of the converter by sampling at a rate much higher than the signal of interest. This spreads the noise out over a wider range in the frequency domain, thereby effectively reducing the racket at any one frequency bin. A 2X oversampling reduces the noise flooring by 3dB.
SFDR is divers as the ratio of the RMS value of an input sine wave to the RMS value of the largest spur observed in the frequency domain using an FFT plot. It is typically expressed in dB. SFDR is of import in certain communication applications that crave maximizing the dynamic range of the ADC. Spurs prevent the ADC from converting small-scale input signals, because the distortion component can be much larger than the bespeak of interest. This limits the dynamic range of the ADC. Note that a large spur in the frequency domain may not significantly affect the SNR, but volition significantly bear on the SFDR.
Final Thoughts
Returning to the ADC example, assume we are measuring DC-type signals and our ADC accepts bipolar input signals. Nosotros choose the B grade of the MAX1241, which has 1LSB DNL fault, 1LSB INL error (0.0244%), 3LSB kickoff error (3/4096 = 0.0732%), and gain of 4LSB (0.0977%). Adding the errors, nosotros obtain a total fault of 0.1953%. We can calibrate out the showtime and gain errors, dropping our error to 0.0244%. Every bit long every bit our voltage-reference error is less than 0.075% - 0.024% = 0.051%, we are within the error upkeep. A 5ppm/°C drift of more than l degrees equates to a 0.025% drift mistake, with a 0.026% error upkeep remaining. For 12-bit operation, we need to have a voltage reference with a voltage-racket specification considerably less than 1LSB (which is 2.5V/4096 = 610µV peak-to-peak or 102µV RMS). The MAX6166 is a good choice with 5ppm/°C drift and 30µV RMS wideband voltage noise. It also has aplenty source and sink current adequacy to bulldoze the ADC (and additional circuitry if needed). Note that the 30µV noise spec equates to 180µV peak-to-peak, which is one-3rd of an LSB at the 12-chip level and one-6th of an LSB at the 11-bit level (which is what our system requirement actually is).
A quick check of the MAX1241 proceeds drift reveals a specification of 0.25ppm/°C or 12.5ppm over a fifty°C temperature change, which is well within spec.
Now we accept a feasible solution that should prevent any hidden performance hiccups due to the specifications. Note for this example that we didn't address the Air-conditioning performance at all. However, with your better understanding of the ADC specs and how they relate to the converter's performance, you lot will exist armed with enough information to select the ADC that will give yous the performance y'all need.
Related Parts
| Related Parts | ||
|---|---|---|
| MAX1290 | 400ksps, +5V, 8-/4-Channel, 12-Scrap ADCs with +two.5V Reference and Parallel Interface | Gratuitous Sample |
| MAX1291 | 250ksps, +3V, 8-/iv-Channel, 12-Fleck ADCs with +2.5V Reference and Parallel Interface | Complimentary Sample |
Source: https://www.maximintegrated.com/en/design/technical-documents/tutorials/7/748.html
0 Response to "adc reference voltage is less than what i want to measure"
Post a Comment